Der Dzhanibekov Effekt
Heute mal etwas aus dem Bereich Physik für Wissbegierige: Der Dzhanibekov Effekt, auch das Tennis Racket Theorem genannt erklärt eine Instabilität rotierender Körper mit drei verschiedenen Trägheitsmomenten. Das Trägheitsmoment gibt den Widerstand eines Körpers gegenüber Änderung seiner Rotationsbewegung an. Es hängt von der jeweiligen Rotationsachse und der Geometrie ab. Das Verständnis der Dynamik klassischer Hamiltonianischer Systeme ist nach wie vor ein entscheidendes Ziel mit einer Vielzahl von Anwendungen, die weit über ihre mathematische Umschreibung hinausgehen. Im Fall von integrierbaren Systemen mit wenigen Freiheitsgraden basiert ein effizienter Ansatz auf einer geometrischen Analyse zur Charakterisierung der dynamischen Eigenschaften des mechanischen Systems. Solche geometrischen Phänomena sind typischerweise der Ursprung für die Robustheit bestimmter Effekte, die experimentell beobachtet werden können. eines davon ist der sog. Dzhanibekov Effekt oder auch Tennisschläger-Effekt genannt.
Dschanibekow-Effekt in der Schwerelosigkeit der ISS
Eine exzellente und detaillierte theoretische Herleitung des Phänomens finden Sie hier (https://arxiv.org/pdf/1606.08237.pdf). Mit einer die ein wenig gröber ist, die dennoch das Phänomen erklärt setzen wir uns hier auseinander. Leider sind hier einige Vorkenntnisse aus der Dynamik starrer Körper notwendig:
Betrachten Sie eine Trägheitsmatrix (diagonalisiert) mit den Trägheitsmomenten I1 und I2 und I3, so dass I1 am kleinsten und I3 am größten ist. Betrachten Sie nun die Bewegung um die Achse des Hauptträgheitsmoments I3. Der Winkelgeschwindigkeitsvektor sei:
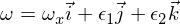
wobei die Epsilons kleine Störungen in den beiden anderen Hauptachsen sind. Wenn man dies nun in die Euler-Gleichungen einfügt, erhält man:
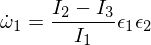
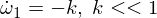
Nun differenzieren wir die zweite Euler-Gleichung:
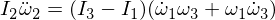
Die Substitution von Omega 1 und Omega 3 in unserem Ausdruck, und da die Multiplikation der Epsilons sie klein genug macht, um sie zu ignorieren,
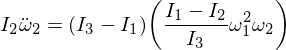
Damit erhalten wir eine Differentialgleichung für Omega 2 der Form:
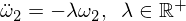
Die Lösung elementar ist:
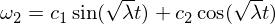
Daher wissen wir, dass die Rotationsstörung in der Omega-1-Achse stabil ist und periodische Bewegungen ausführt, oder in der Terminologie der Starrkörperbewegung, dass sie eine Präzession ausführt. Die Störung in Omega 3 folgt einem ähnlichen Argument wie oben, und ich überlasse es Ihnen als Übung, sie durchzuarbeiten. Für die Zwischenachse haben wir:
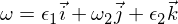
Eingesetzt in die Euler-Gleichungen:
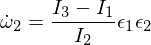
Differenzierung der dritten Euler-Gleichung ergibt:
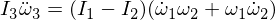
Ersetzen wir unsere abgeleiteten Ausdrücke:
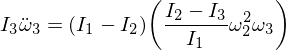
Nun neu anordnen, und leiten wir die folgende Differentialgleichung ab:
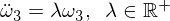
Beachten Sie, dass der Koeffizient jetzt positiv ist, was daher zu exponentiellen Lösungen führt:
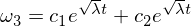
Diese Lösung zeigt, dass Omega 3 unter einer Störung von Omega 2 entlang der Zwischenachse instabil ist!
Was bedeutet das?
Jetzt können wir alles, was wir zum Verständnis des Theorems abgeleitet und gelernt haben, miteinander verknüpfen. Einfach ausgedrückt: Wenn die Rotation entlang der Zwischenachse gestört ist, ergibt sich eine Differentialgleichung mit exponentiellen Lösungen. Dies führt zu einer instabilen Bewegung, im Gegensatz zu der in den beiden anderen Achsen beobachteten präzessiven Bewegung. Dieses Ergebnis ist ziemlich überraschend. Es gibt keine intuitive Unterstützung für ein solches Theorem, da wir uns nicht vorstellen können, warum das dazwischenliegende Trägheitsmoment zu einer instabilen Rotation führen würde. Es scheint, als ob es rein mathematischer Natur ist.